En el estudio del clima, Edward Lorenz descubrió que pequeñas variaciones en las condiciones iniciales podían generar resultados drásticamente diferentes, incluso dentro de sistemas deterministas.
Ese hallazgo, conocido como efecto mariposa, dio origen al concepto moderno de caos determinista.
Curiosamente, esa misma lógica puede observarse en un sistema mucho más simple: la dinámica poblacional descrita por la ecuación logística:
X_{n+1} = r * X_n(1 - X_n)
donde:
- ( x_n ) representa la población normalizada en el tiempo ( n ),
- ( r ) es el parámetro de crecimiento,
- y el término ( (1 - x_n) ) introduce un límite ambiental.
Para analizar la evolución de este sistema y visualizar sus comportamientos (estables o caóticos), se puede implementar una función en Python que calcule la secuencia poblacional:
def poblacion(r, x_0, cota):
"""
Calcula la evolución de una población según el modelo logístico:
x_{n+1} = r * x_n * (1 - x_n)
Parámetros:
r (float): Tasa de crecimiento.
x_0 (float): Valor inicial de la población (entre 0 y 1).
cota (float): Tolerancia para considerar que se alcanzó la estabilización.
Retorna:
valor_estable (float): Valor final de estabilización.
iteraciones (int): Número de iteraciones realizadas.
evolucion (list): Lista con los valores de evolución.
"""
evolucion = [x_0]
while True:
x_p = r * evolucion[-1] * (1 - evolucion[-1])
evolucion.append(x_p)
# Condición de estabilidad
if abs(evolucion[-1] - evolucion[-2]) <= cota:
break
# Evita bucles infinitos
if len(evolucion) > 500:
break
valor_estable = evolucion[-1]
iteraciones = len(evolucion)
return valor_estable, iteraciones, evolucion
Régimen no caótico: equilibrio y estabilidad
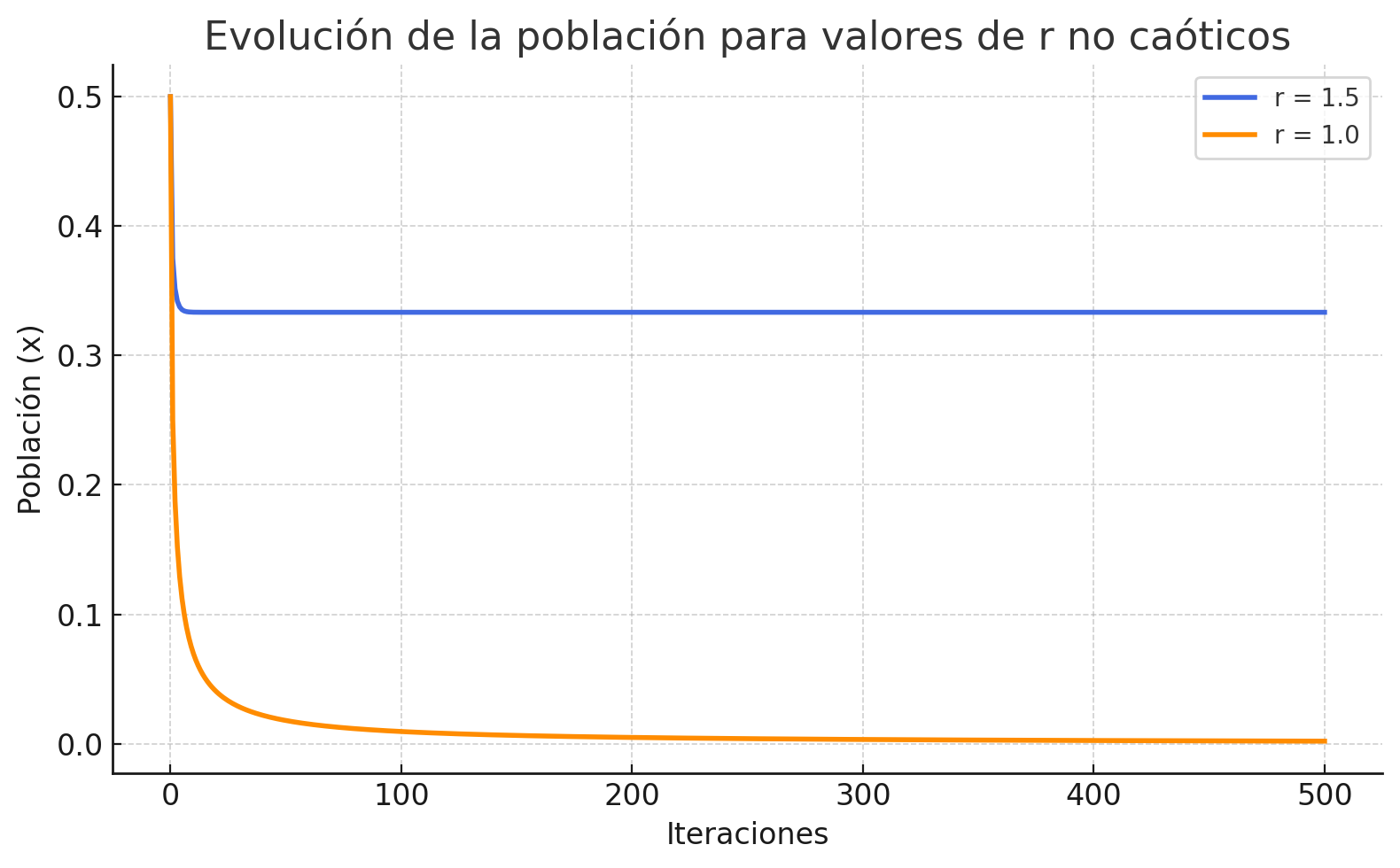
Cuando los valores de ( r ) son pequeños —por ejemplo, ( r = 1.0 ) o ( r = 1.5 )— el sistema converge rápidamente hacia un punto de equilibrio.
En este régimen no caótico, cualquier población inicial tenderá a estabilizarse en un mismo valor final, independientemente de pequeñas diferencias en ( x_0 ).
Visualmente, las trayectorias se aplanan hacia un valor fijo.
Esto representa un entorno predecible:
- La población alcanza un tamaño estable.
- El comportamiento a largo plazo puede anticiparse fácilmente.
En términos meteorológicos, este escenario se asemeja a un sistema atmosférico estable, donde pequeñas perturbaciones se disipan y el clima retorna a su estado medio: un ejemplo de orden, equilibrio y previsibilidad.
Representación gráfica del régimen no caótico
Régimen caótico: sensibilidad y divergencia
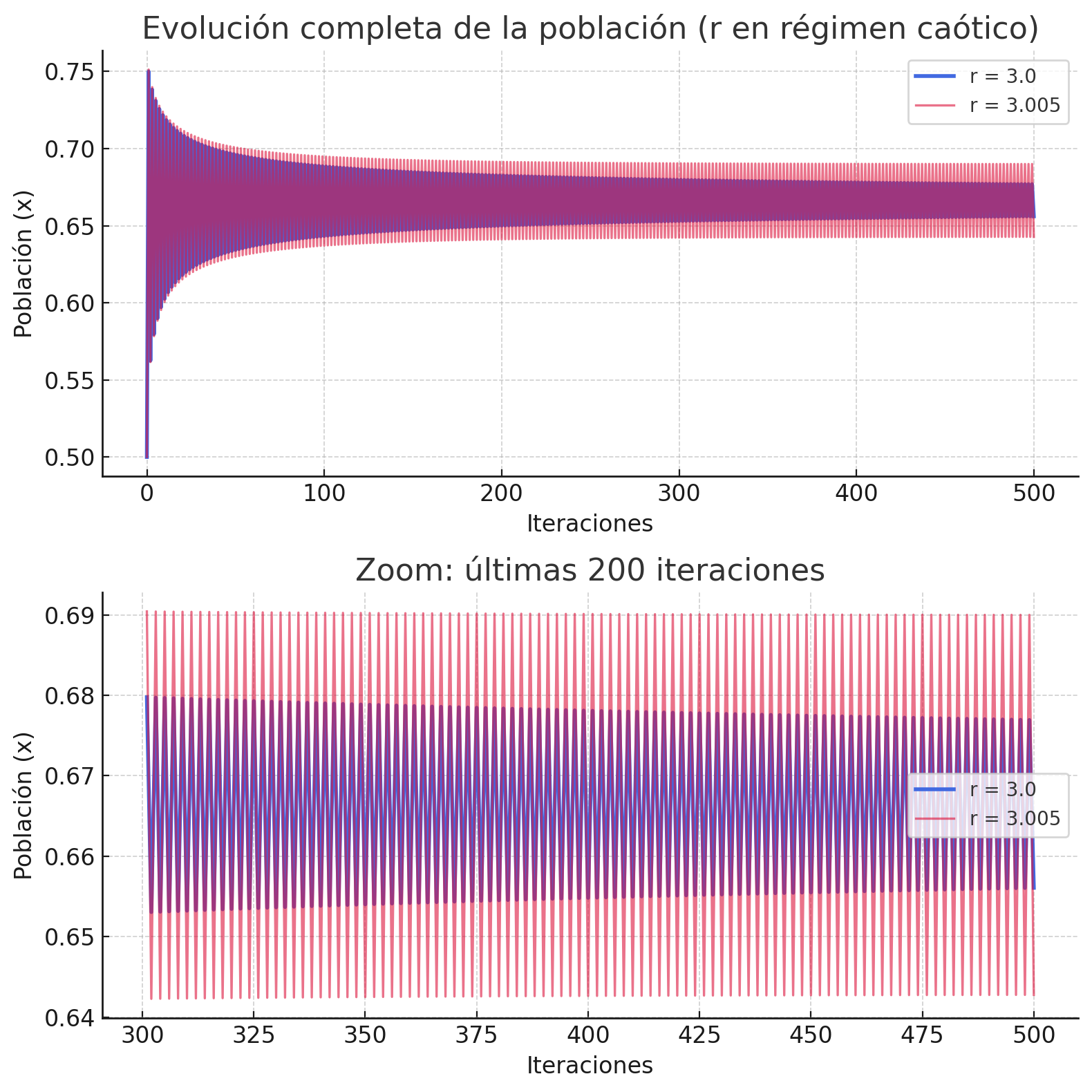
Cuando aumentamos ligeramente el parámetro a valores como ( r = 3.0 ) o ( r = 3.005 ), la situación cambia radicalmente.
El sistema deja de estabilizarse: aparece una oscilación periódica que luego se vuelve aperiódica y caótica.
Pequeñas diferencias en ( r ) o en la condición inicial generan trayectorias que divergen rápidamente con el tiempo.
En la gráfica, ambas curvas parten del mismo punto pero acaban describiendo movimientos completamente diferentes.
Aunque la ecuación es determinista, su evolución se vuelve prácticamente impredecible.
Aquí es donde la analogía meteorológica se hace evidente:
el comportamiento de la atmósfera, como el de estas poblaciones, obedece reglas deterministas, pero la extrema sensibilidad a las condiciones iniciales hace que el pronóstico a largo plazo se vuelva imposible.
Un cambio minúsculo —una milésima en ( r ), una perturbación de temperatura— puede alterar completamente la evolución del sistema.
Representación gráfica del régimen caótico
Tanto en las ecuaciones meteorológicas como en el modelo logístico, el caos no significa desorden absoluto, sino complejidad dentro de un sistema perfectamente determinista.
La ecuación sigue siendo la misma; lo que cambia es la relación entre sus variables.
Este paralelismo entre el clima y las poblaciones revela una verdad profunda:
La predictibilidad no depende de conocer las leyes, sino de la estabilidad del sistema que esas leyes describen.