La predecibilidad es a la prediccion como el romance es al sexo
¿Has notado que a veces el pronóstico del tiempo indica lluvia y termina siendo un día soleado? ¿O que la temperatura prevista difiere significativamente de la real? Estos “fallos” en las predicciones meteorológicas no son simples errores, sino manifestaciones de la complejidad inherente a la predicción del tiempo. En este artículo, exploraremos en profundidad cómo la meteorología moderna ha evolucionado desde los modelos deterministas hacia las predicciones por conjuntos, una transformación que nos permite no solo pronosticar el tiempo, sino también entender y cuantificar la incertidumbre en nuestras predicciones.
Los modelos deterministas en meteorología parten de datos medidos —temperatura, presión, humedad— y producen un único estado futuro. Esa aparente solidez choca con la realidad: pequeñas imprecisiones en las condiciones iniciales o en los parámetros del modelo, combinadas con la no linealidad de las ecuaciones atmosféricas, se propagan y amplifican con el tiempo, dando lugar a previsiones que divergen rápidamente. Para una discusión más amplia sobre la sensibilidad a las condiciones iniciales y el caos determinista, consulta el post Caos.
Para ilustrar la sensibilidad a las condiciones iniciales puede servir un análogo en dinámica de poblaciones, por ejemplo:
Xn = r X0 (1 - X0)
donde X0 ∈ (0,1) es la población inicial, r el parámetro de reproducción y Xn la población en el tiempo n. Según r, el sistema muestra regímenes distintos e incluso comportamiento caótico: pequeñas diferencias en X0 pueden producir trayectorias muy diferentes.
La predicción por conjuntos surge como respuesta práctica a esta incertidumbre. En lugar de aceptar un único resultado X(t0 + t’), buscamos una distribución de probabilidad ρ(t0 + t’) que describa los estados posibles:
X(t0 + t') ⟹ ρ(t0 + t')

En la práctica esto se hace generando muchas simulaciones con ligeras variaciones en las condiciones iniciales o en parámetros. El proceso habitual consiste en definir intervalos plausibles para cada variable medida, por ejemplo:
Temperatura: [T0 - ΔT, T0 + ΔT]
Presión: [P0 - ΔP, P0 + ΔP]
Humedad: [H0 - ΔH, H0 + ΔH]
y crear vectores de estado local Vᵢ = (xᵢ, yᵢ, …, zᵢ) que, al integrarse en el modelo, generan una colección de estados Xᵢ que conforman la distribución empírica del futuro atmosférico.
Esta distribución permite cuantificar incertidumbre y extraer estadísticas útiles. La media, por ejemplo, puede calcularse en el caso continuo como
x = ∫ x ρ(x) dx
o en el caso discreto a partir de un conjunto finito de predicciones como
x = (1/ N) Σ xᵢ
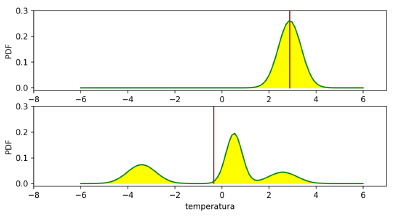
Sin embargo, conviene recordar la paradoja del valor medio: la media puede situarse en regiones de probabilidad muy baja o representar un estado físicamente improbable que no coincide con ninguno de los escenarios individuales. Por eso es importante complementar la media con medidas de dispersión (varianza, percentiles) y analizar la forma de la distribución para identificar múltiples modos, colas pesadas o valores atípicos que podrían anticipar eventos extremos.
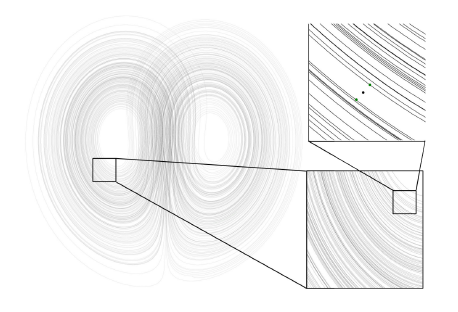
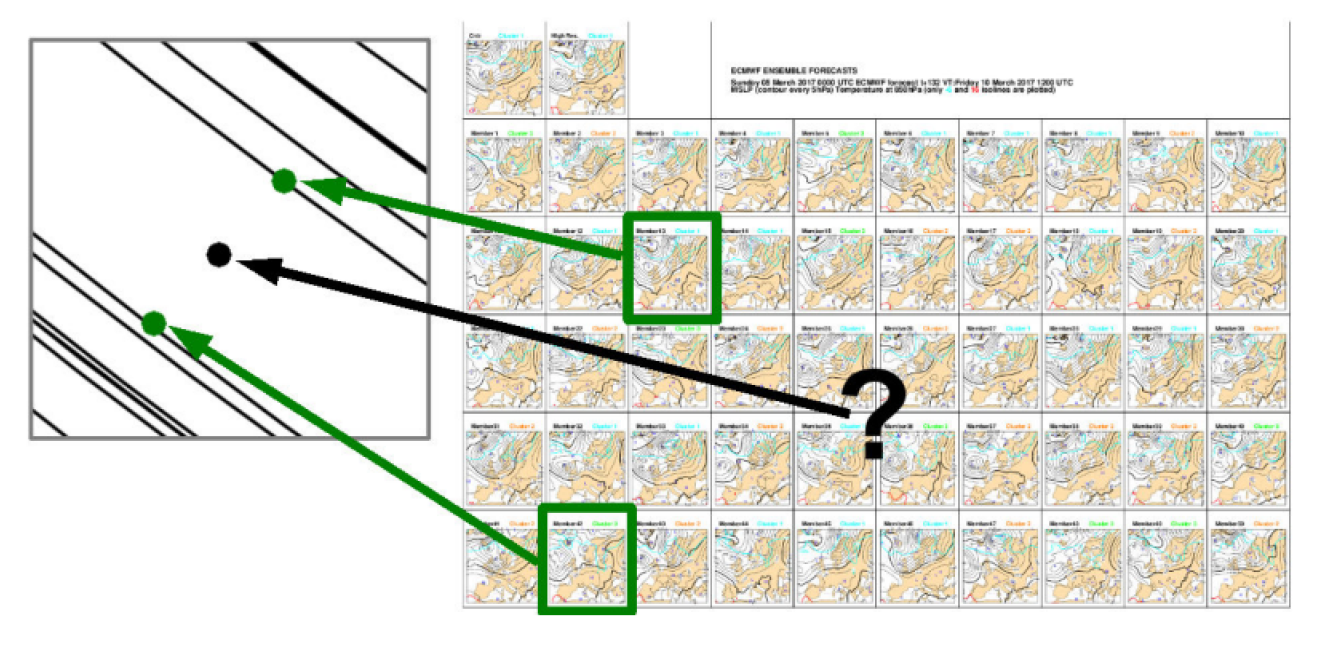
La manera en que las predicciones se dispersan nos revela aspectos fundamentales sobre la atmósfera y nuestra capacidad de predicción. Para cuantificar esta dispersión, utilizamos la varianza, que se puede calcular de dos formas según trabajemos con datos discretos (σ² = (1/√(N-1)) Σ(xᵢ - x)²) o continuos (σ² = ∫(x - x)²ρ(x)dx).
Pero más allá de las fórmulas, lo verdaderamente fascinante es su interpretación. Cuando encontramos una baja dispersión, generalmente estamos ante una atmósfera estable, típica de situaciones anticiclónicas donde las predicciones tienden a ser más fiables. Por otro lado, una alta dispersión nos alerta de una situación más compleja: la atmósfera está inestable, y nuestras predicciones son menos certeras.
Los valores atípicos que encontramos en estas distribuciones merecen una atención especial. Aunque podríamos estar tentados a descartarlos como errores, a menudo son señales de posibles eventos extremos que, aunque poco probables, podrían tener un impacto significativo. Por ejemplo, una predicción que se desvía considerablemente podría estar anticipando una tormenta severa o un cambio brusco de temperatura.
Métodos Alternativos y su Evolución
Antes de que se establecieran los fundamentos matemáticos de los Sistemas de Predicción por Conjuntos (SPC), los meteorólogos ya exploraban formas ingeniosas de mejorar sus predicciones. Uno de los métodos más interesantes consistía en ejecutar el mismo modelo meteorológico múltiples veces, pero con diferentes datos de partida. Este enfoque, aunque más subjetivo, permitía a los expertos desarrollar una intuición sobre la consistencia de sus predicciones.
Sin embargo, este método tenía sus limitaciones. Al depender fuertemente de la interpretación personal del meteorólogo y carecer de parámetros estadísticos formales, resultaba difícil cuantificar la fiabilidad de las predicciones de manera objetiva.
Una aproximación alternativa, que aún hoy resulta valiosa, es la comparación entre diferentes modelos de predicción. Esta técnica reconoce una realidad fundamental: no todos los modelos se comportan igual en todas las situaciones. De hecho, un mismo modelo puede mostrar discrepancias considerables ante situaciones aparentemente similares. La clave está en considerar las características específicas de cada modelo, como su resolución o su capacidad para tener en cuenta la orografía del terreno, algo especialmente crucial cuando se trata de predecir precipitaciones.
El Huerto: Un Caso Práctico que lo Ilustra Todo
Para entender mejor cómo estos conceptos se aplican en el mundo real, consideremos el caso de un pequeño huerto. Imaginemos que necesitamos saber si las temperaturas nocturnas bajarán del punto de congelación, lo que podría devastar nuestra cosecha. Es aquí donde la diferencia entre los enfoques determinista y probabilístico se vuelve crucial.
Un modelo determinista nos daría una única respuesta: “La temperatura será de -1°C”. Con esta información, probablemente tomaríamos medidas para proteger nuestros cultivos. Pero, ¿qué pasa si ese único valor predicho es el resultado de un error en las condiciones iniciales?

En cambio, un sistema de predicción por conjuntos nos proporcionaría una imagen más completa: podríamos ver que, de todas las simulaciones realizadas, solo un 30% predice temperaturas bajo cero, mientras que la mayoría sugiere temperaturas entre 1°C y 3°C. Esta información nos permite tomar una decisión más informada, considerando tanto el riesgo como la probabilidad de helada.
El viaje desde los modelos deterministas hasta las predicciones por conjuntos marca un antes y un después en la historia de la meteorología. Este cambio de paradigma no solo ha revolucionado nuestra forma de predecir el tiempo, sino que ha transformado fundamentalmente nuestra comprensión de la atmósfera y sus caprichos.
La capacidad de cuantificar la incertidumbre ha sido quizás el avance más significativo. Ya no nos limitamos a decir “mañana lloverá”, sino que podemos expresar con precisión la probabilidad de precipitación y, lo que es más importante, entender qué tan seguros estamos de esa predicción. Esta nueva perspectiva nos permite identificar diferentes escenarios posibles y calcular sus probabilidades asociadas, proporcionando una imagen mucho más rica y matizada del tiempo venidero.
En la práctica, estos avances se traducen en predicciones más fiables y en una mejor capacidad para detectar eventos extremos. Los meteorólogos pueden ahora tomar decisiones más informadas y, lo que es crucial, comunicar mejor la incertidumbre al público. Cuando un meteorólogo nos advierte sobre una posible tormenta severa, no solo nos está diciendo qué podría pasar, sino también cuán probable es que ocurra.
Sin embargo, sería ingenuo pensar que hemos resuelto todos los desafíos de la predicción meteorológica. Los modelos, por muy sofisticados que sean, siguen teniendo sus limitaciones. Las mediciones que alimentan estos modelos contienen inevitablemente pequeñas incertidumbres, y la atmósfera, con su naturaleza caótica y compleja, continúa desafiando nuestra capacidad de predicción a largo plazo.
Mirando hacia el futuro, el camino es prometedor. Los avances en tecnología nos permitirán desarrollar modelos cada vez más sofisticados, capaces de integrar y procesar cantidades masivas de datos con mayor precisión. La cuantificación de la incertidumbre seguirá mejorando, y con ella, nuestra capacidad para tomar decisiones informadas en situaciones meteorológicas críticas.
La meteorología moderna es un testimonio del poder de combinar la observación científica rigurosa con el análisis estadístico avanzado. Las predicciones por conjuntos no son solo una herramienta más en el arsenal del meteorólogo; representan una nueva forma de entender y comunicar la incertidumbre inherente en el comportamiento de la atmósfera.