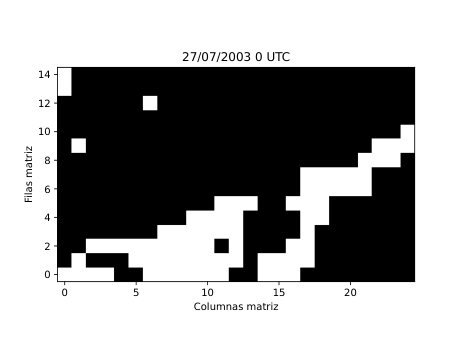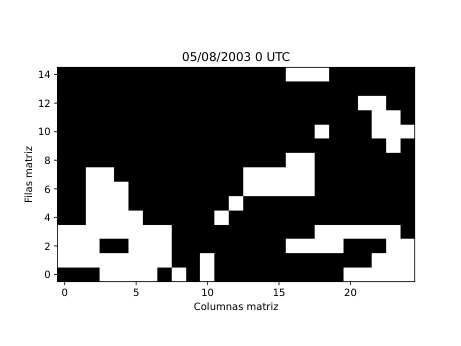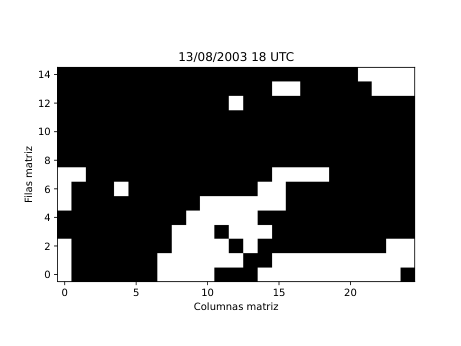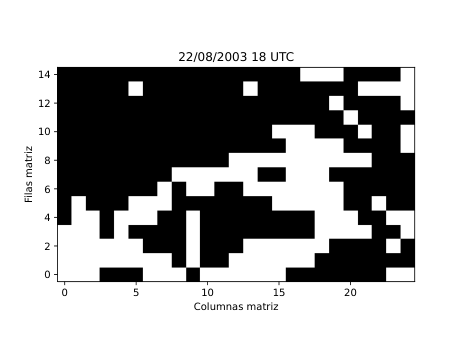
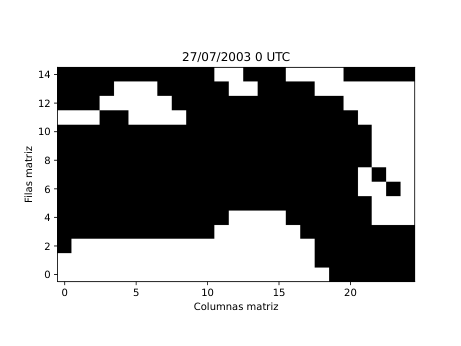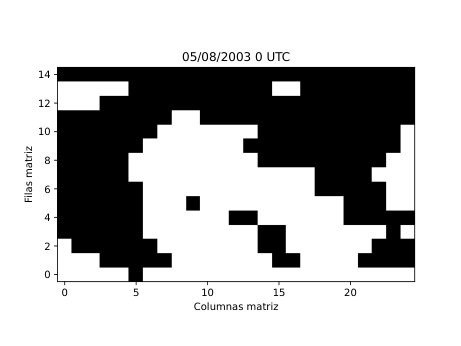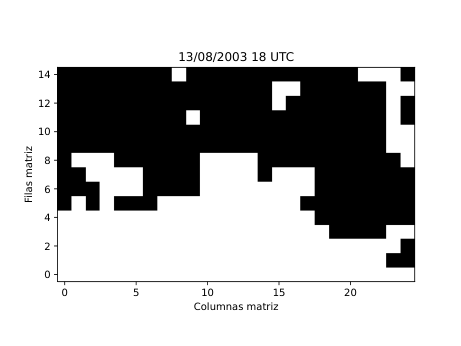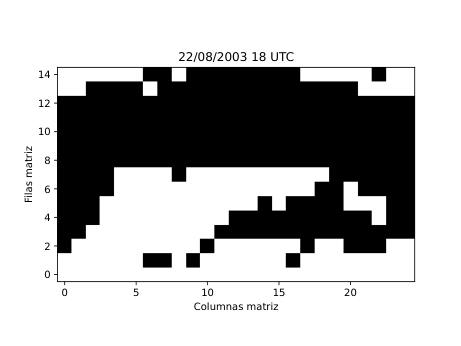
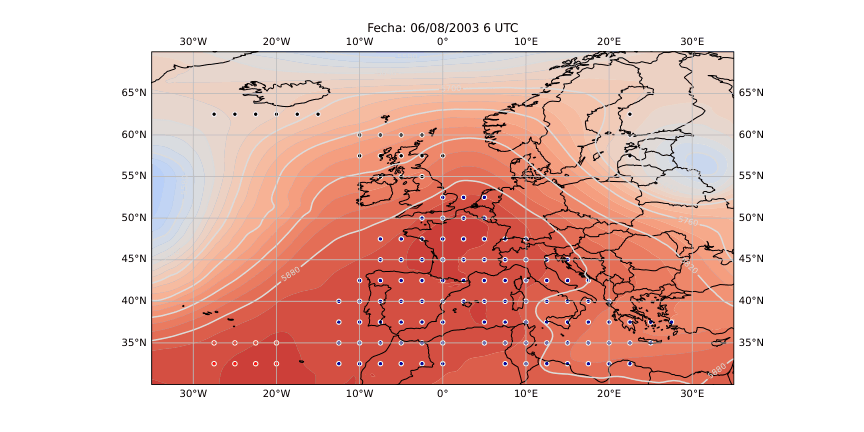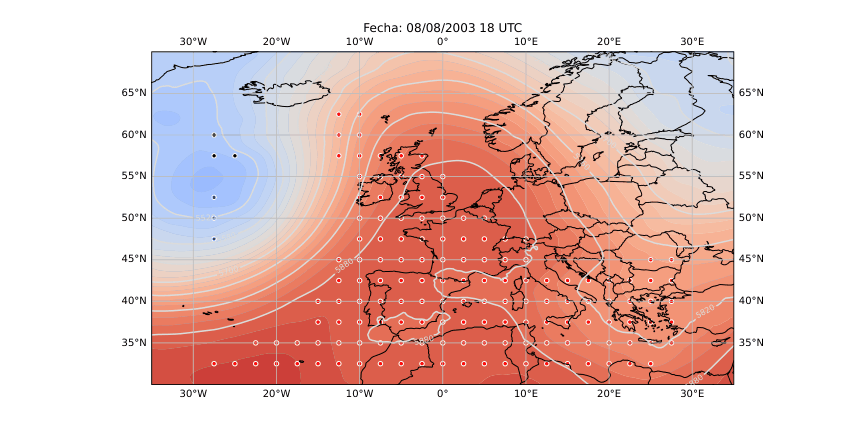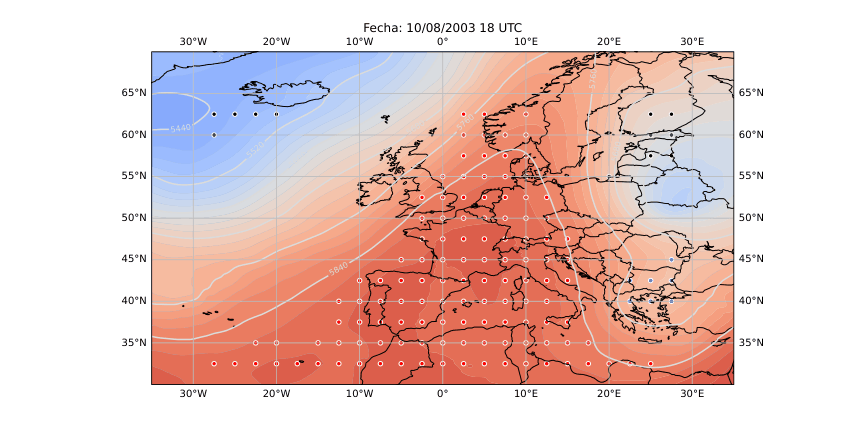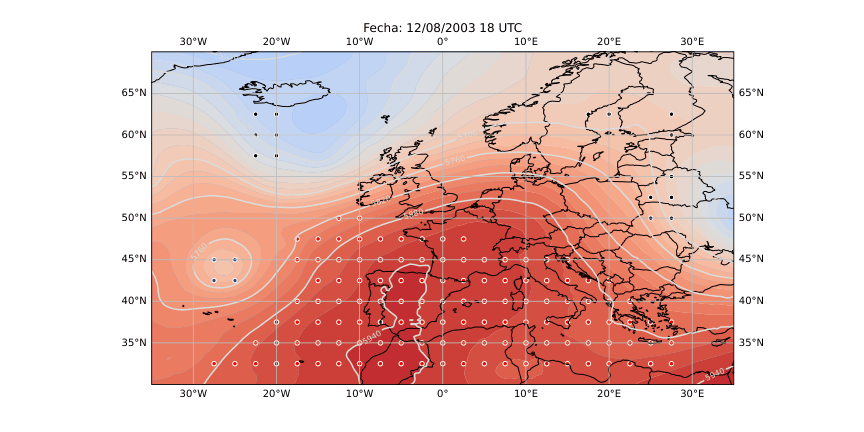
Figura 28
Durante los últimos años, los fenómenos meteorológicos extremos —olas de calor, olas de frío, sequías o inundaciones— se han hecho cada vez más frecuentes e intensos. Detrás de muchos de ellos se encuentra un patrón atmosférico fascinante y complejo: el bloqueo atmosférico. Estos bloqueos son grandes estructuras de alta presión que interrumpen el flujo normal del aire, desviando las corrientes y haciendo que determinadas masas de aire queden estancadas sobre una región durante días o semanas. Su efecto puede ser devastador, ya que pueden generar olas de calor persistentes o impedir la llegada de frentes lluviosos durante largos periodos.
Como físico y apasionado de la meteorología, decidí centrar mi Trabajo Fin de Grado en estos bloqueos, pero desde una perspectiva diferente a la habitual. En la mayoría de los estudios, la atmósfera se analiza desde un punto fijo del espacio, utilizando lo que se conoce como un enfoque euleriano. Este tipo de análisis examina cómo cambian en el tiempo variables como la altura geopotencial a 500 hPa o la vorticidad potencial en un punto dado, lo que permite detectar zonas de alta o baja presión y patrones de circulación anómalos. Sin embargo, este enfoque observa la atmósfera “desde fuera”, sin seguir el movimiento real del aire.
Mi propuesta fue cambiar de punto de vista y mirar la atmósfera “desde dentro”, siguiendo las trayectorias de las masas de aire. Para ello adopté un enfoque lagrangiano, que consiste en estudiar el movimiento de las partículas a medida que se desplazan por la atmósfera. Este método permite observar directamente dónde el flujo se frena, se desvía o queda atrapado, sin necesidad de imponer a priori una definición geométrica o dinámica del bloqueo. En otras palabras, deja que sean las trayectorias las que hablen.
El desarrollo del método se basó en el uso del software HYSPLIT (Hybrid Single-Particle Lagrangian Integrated Trajectory), una herramienta de la NOAA diseñada para calcular trayectorias de partículas en la atmósfera. A partir de los datos del reanálisis ERA5 del Centro Europeo de Predicción a Medio Plazo (ECMWF), generé miles de retrotrayectorias de partículas virtuales en la atmósfera media (Figura 14), alrededor de los 500 hPa (unos 5.500 metros de altitud). Con estas trayectorias obtuve tres variables principales: la distancia end-to-end, que mide cuánto se separa el punto final del inicial y sirve como indicador del grado de estancamiento del aire (Figura 20); la longitud total de la trayectoria, que representa la distancia total recorrida por la partícula (Figura 21); y las proyecciones zonal y meridional, que muestran cuánto se ha desplazado el aire en dirección este-oeste y norte-sur respectivamente. En condiciones de bloqueo, la proyección zonal tiende a reducirse mientras que la meridional aumenta, ya que el aire deja de avanzar hacia el este y se desvía hacia latitudes distintas.
A partir de estos parámetros elaboré mapas y series temporales (Figura 25 y 26) que reflejan la evolución de los flujos en la región de estudio. Para identificar espacialmente las áreas bloqueadas (Figura 28) utilicé el algoritmo de agrupamiento DBSCAN, que permite detectar grupos de puntos con características similares basándose en la densidad de los datos. De esta forma fue posible aislar las zonas donde el flujo atmosférico mostraba un claro estancamiento y representarlas directamente sobre mapas de altura geopotencial.
El método se puso a prueba con un caso emblemático: la ola de calor europea del verano de 2003, uno de los eventos meteorológicos más extremos registrados en las últimas décadas. Entre el 6 y el 12 de agosto de aquel año, se formó un intenso anticiclón sobre Europa occidental que impidió la entrada de aire fresco y favoreció temperaturas récord en buena parte del continente. El modelo lagrangiano detectó con precisión esa región bloqueada, coincidiendo con los patrones de alta presión observados en los mapas sinópticos tradicionales. También se aplicó de forma preliminar al episodio de junio de 2019, que presentó varias olas de calor consecutivas. Aunque el método aún necesita ajustes para generalizar y captar múltiples episodios seguidos, los resultados fueron coherentes y alentadores.
Lo interesante de este enfoque es que no depende de un índice o umbral fijo (aunque por el momento sí), como ocurre con métodos tradicionales —por ejemplo, el de Tibaldi y Molteni—, sino que se apoya directamente en el movimiento de las masas de aire. Esto permite observar el bloqueo como un fenómeno dinámico y tangible, una consecuencia natural del flujo atmosférico, y no solo como una anomalía numérica en un campo meteorológico. Además, al ser un método explícito y cuantificable, resulta fácilmente adaptable a procedimientos automáticos y a técnicas modernas de análisis como el machine learning o las redes neuronales convolucionales (CNN).
Los resultados obtenidos (Figura 28) muestran que este tipo de análisis lagrangiano puede ofrecer una visión mucho más intuitiva de la dinámica atmosférica. Permite seguir cómo se forma, evoluciona y disuelve un bloqueo, observando el comportamiento real del aire en movimiento. Sin embargo, para consolidar el método es necesario aplicarlo a un número mayor de episodios y ampliar el periodo de análisis a varias décadas, lo que permitirá estudiar la frecuencia, duración e intensidad de los bloqueos en el contexto del cambio climático. También se abre la posibilidad de automatizar la detección de los patrones de bloqueo más comunes, como los de tipo Omega o Rex, a través de modelos de aprendizaje profundo.
En definitiva, este trabajo propone una manera distinta de estudiar los bloqueos atmosféricos: no observándolos desde fuera, sino viajando con el propio aire. La atmósfera es un sistema dinámico, complejo y no lineal, donde los bloqueos representan una de sus manifestaciones más influyentes. Comprenderlos en detalle es esencial para anticipar los impactos de los fenómenos extremos sobre la sociedad y el medio ambiente. Confío en que los métodos lagrangianos, como el que he desarrollado, se conviertan en una herramienta clave para mejorar nuestra capacidad de observación, análisis y predicción en un clima en constante cambio.
Si te interesa profundizar en lo que comento en esta entrada, puedes visitar mi página de GitHub, donde encontrarás el trabajo completo en formato PDF. Actualmente sigo desarrollando esta línea de investigación, con el objetivo de generalizar el método a cualquier episodio mediante técnicas de Deep Learning. Si tienes alguna duda, sugerencia o simplemente quieres comentar algún detalle, no dudes en escribirme a mi correo. Toda aportación o intercambio de ideas será muy bien recibida.
Los mapas mostrados no incluyen su correspondiente escala de color, lo que puede generar dudas sobre lo que se representa en cada figura. Debido a limitaciones de formato, no me ha sido posible incorporarlas aquí. Sin embargo, invito a quienes estén interesados a visitar mi repositorio de GitHub, donde podrán encontrar los mapas con sus barras de color y un análisis detallado de cada uno de los resultados.
Figura 14
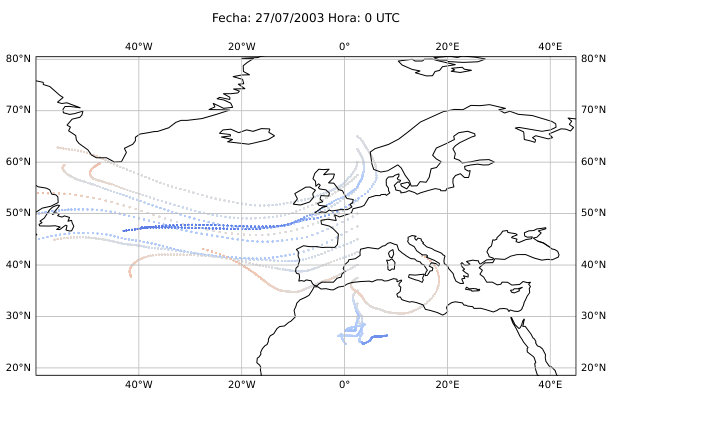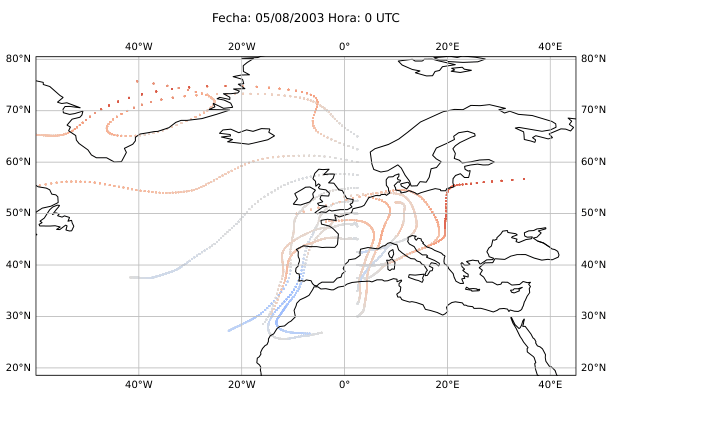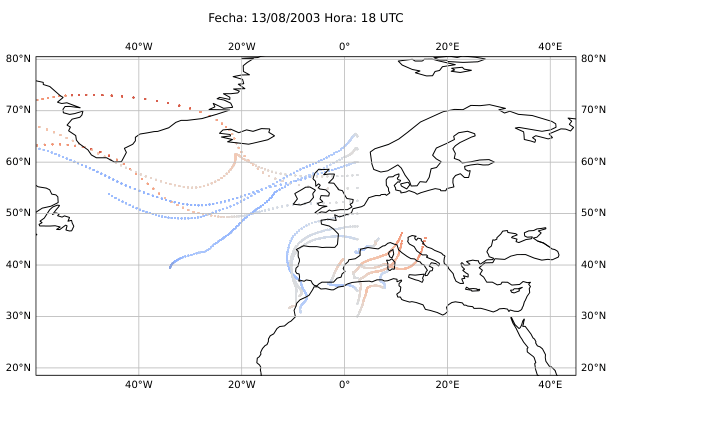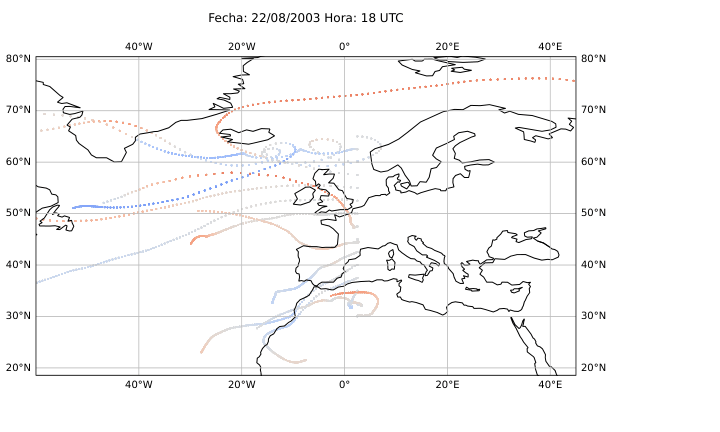
Figura 20
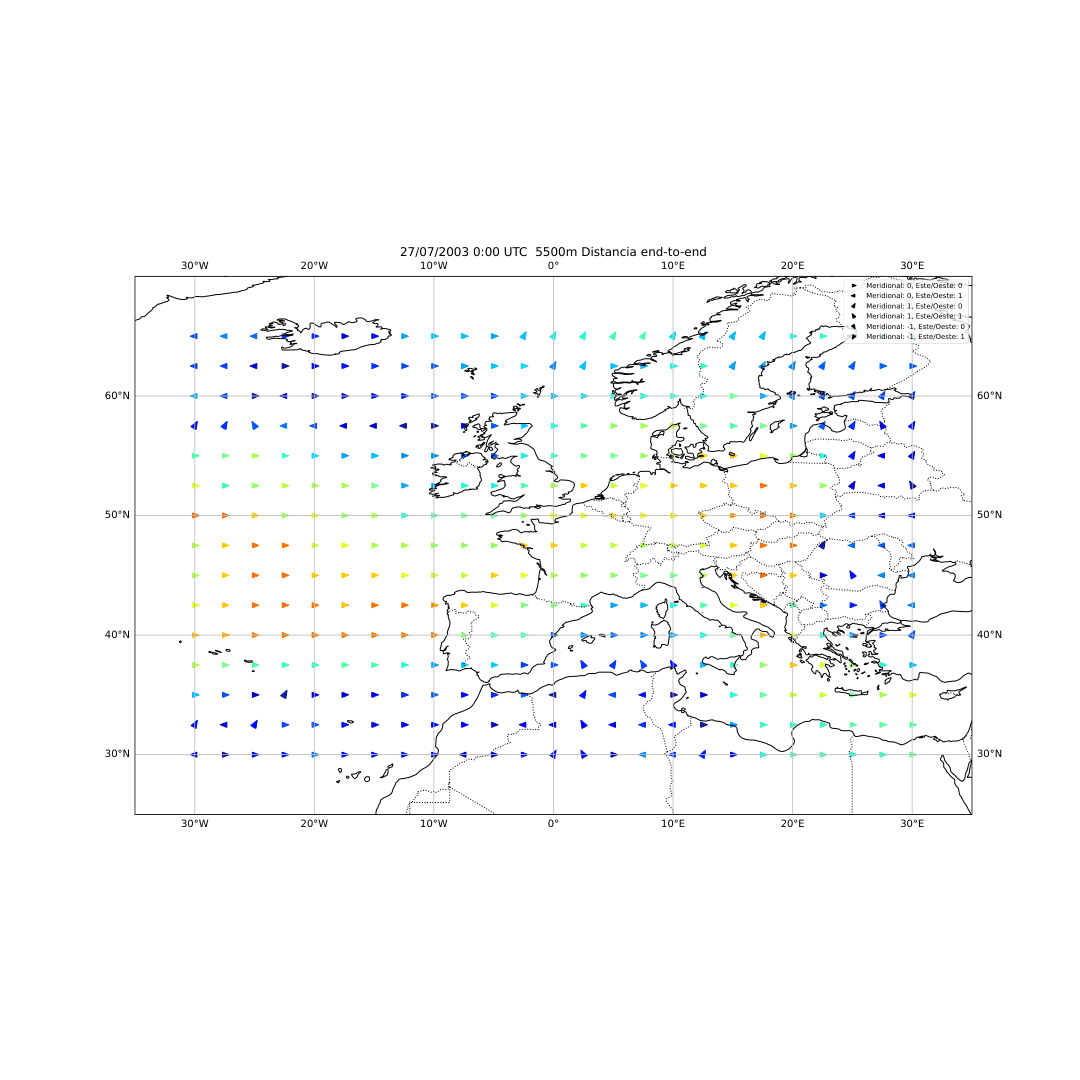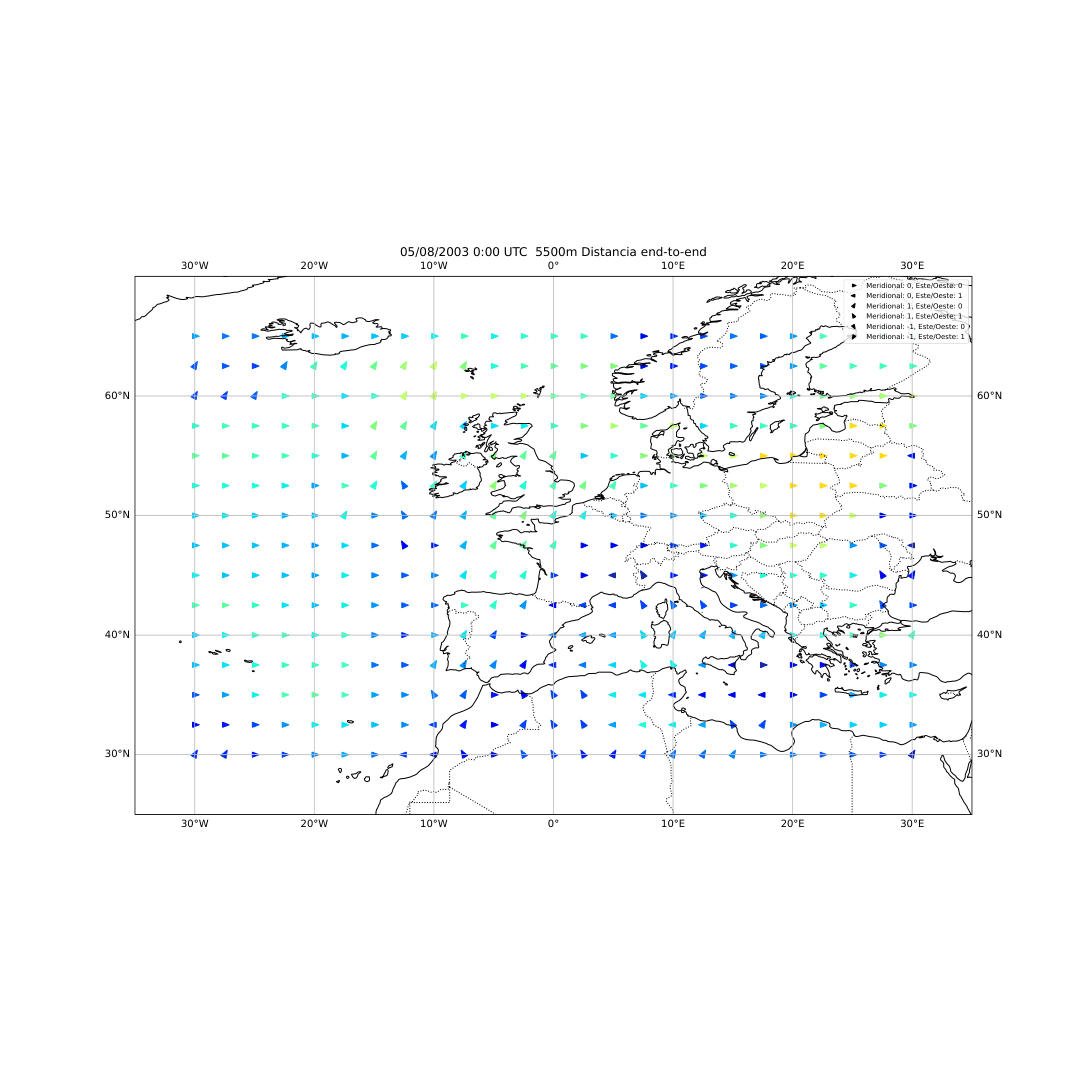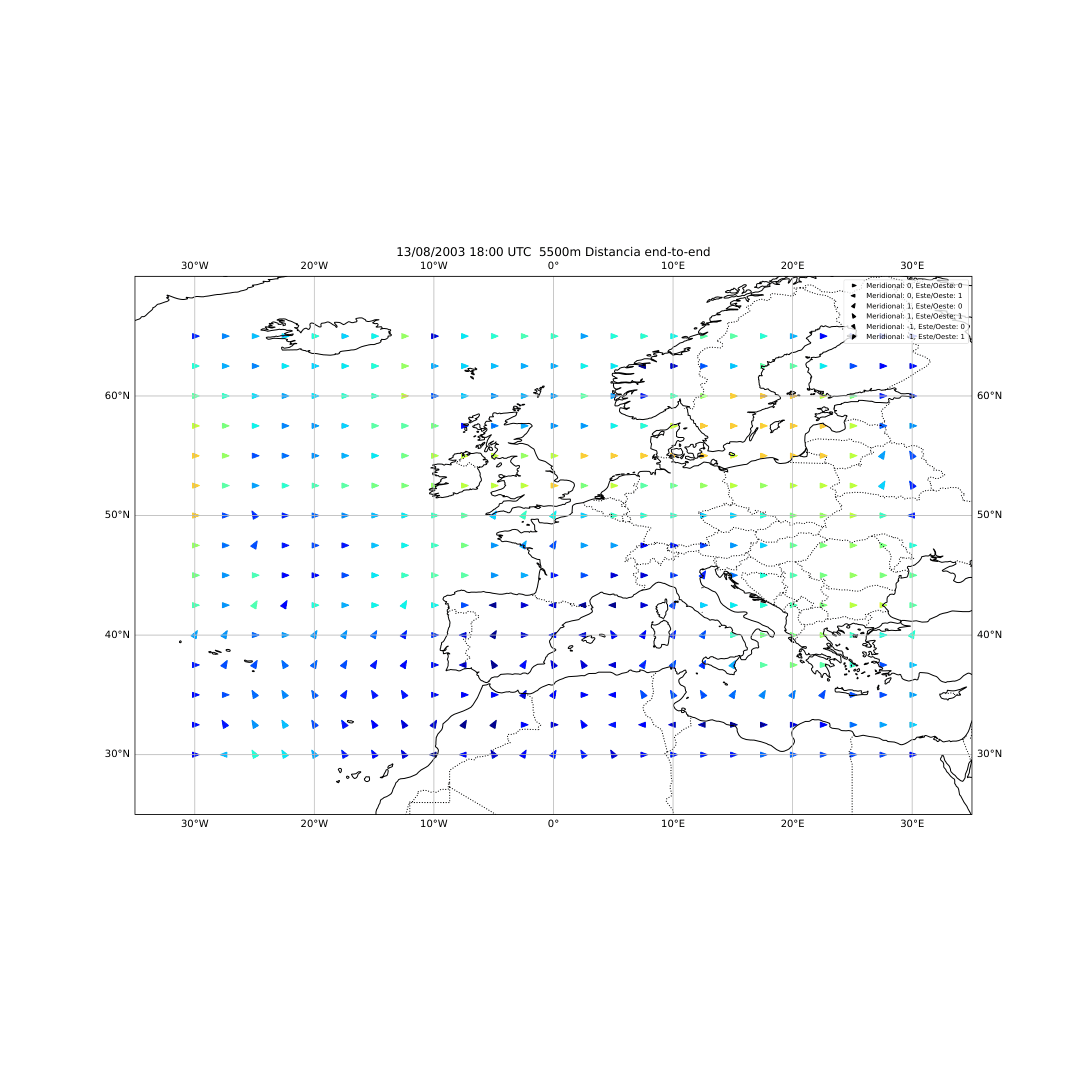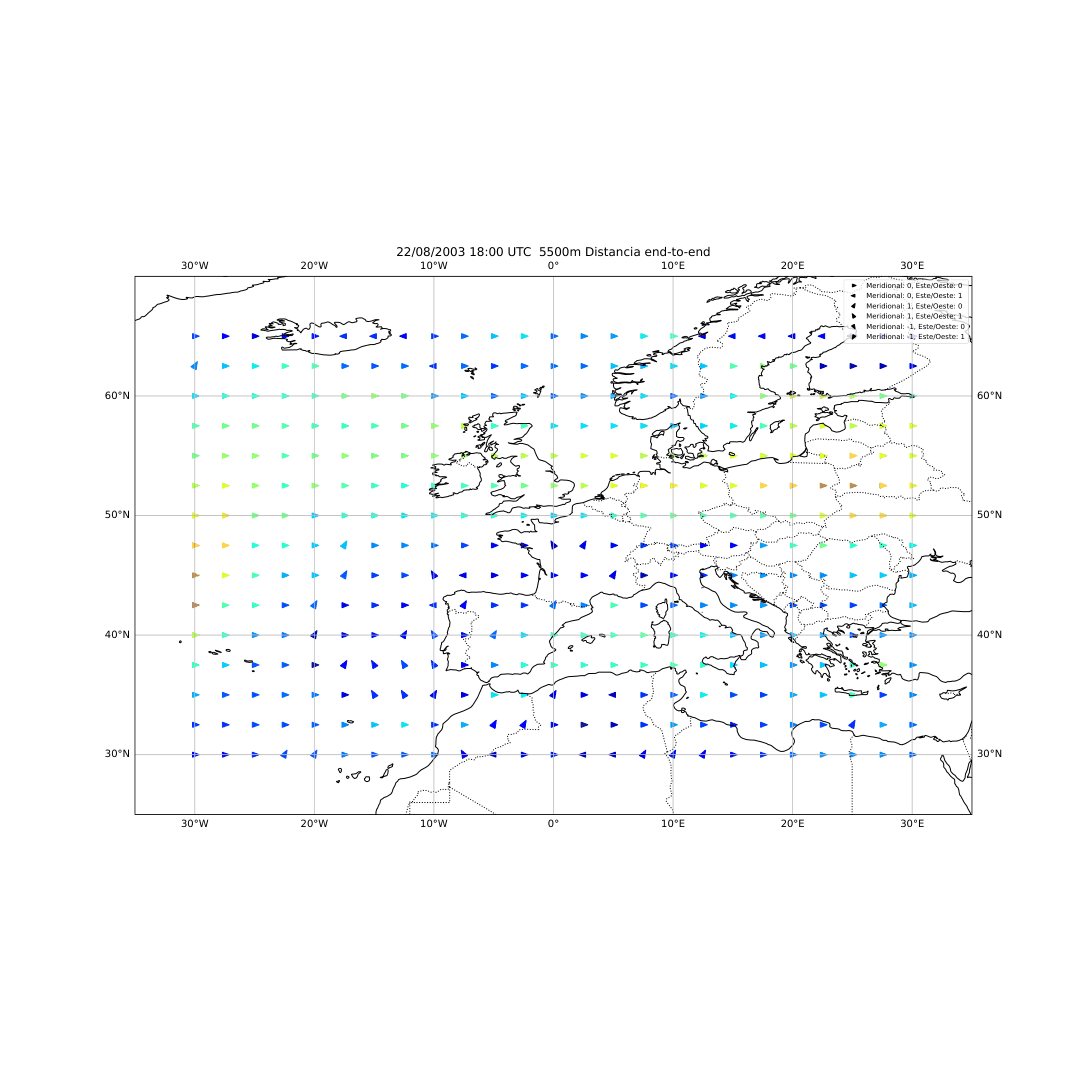
Figura 21
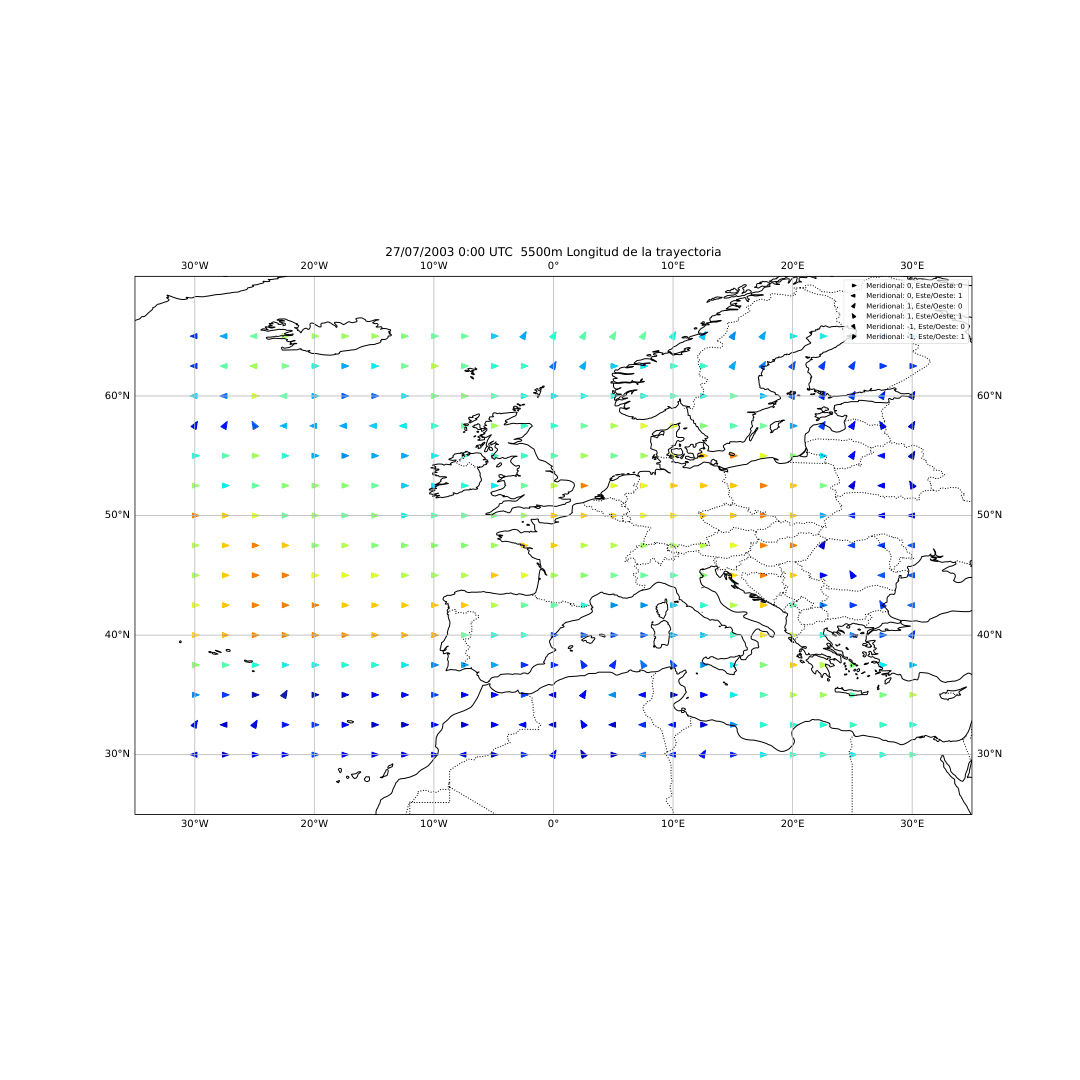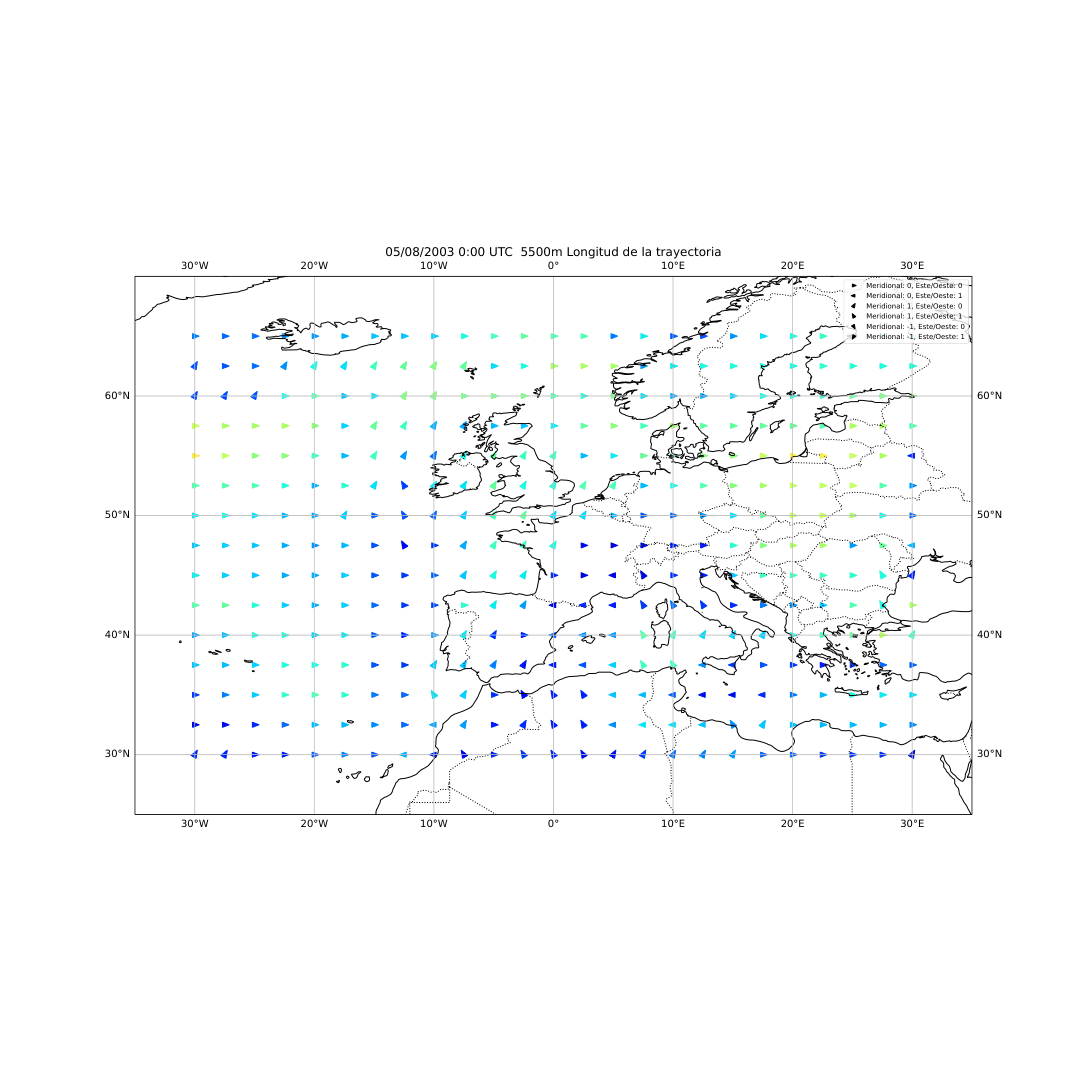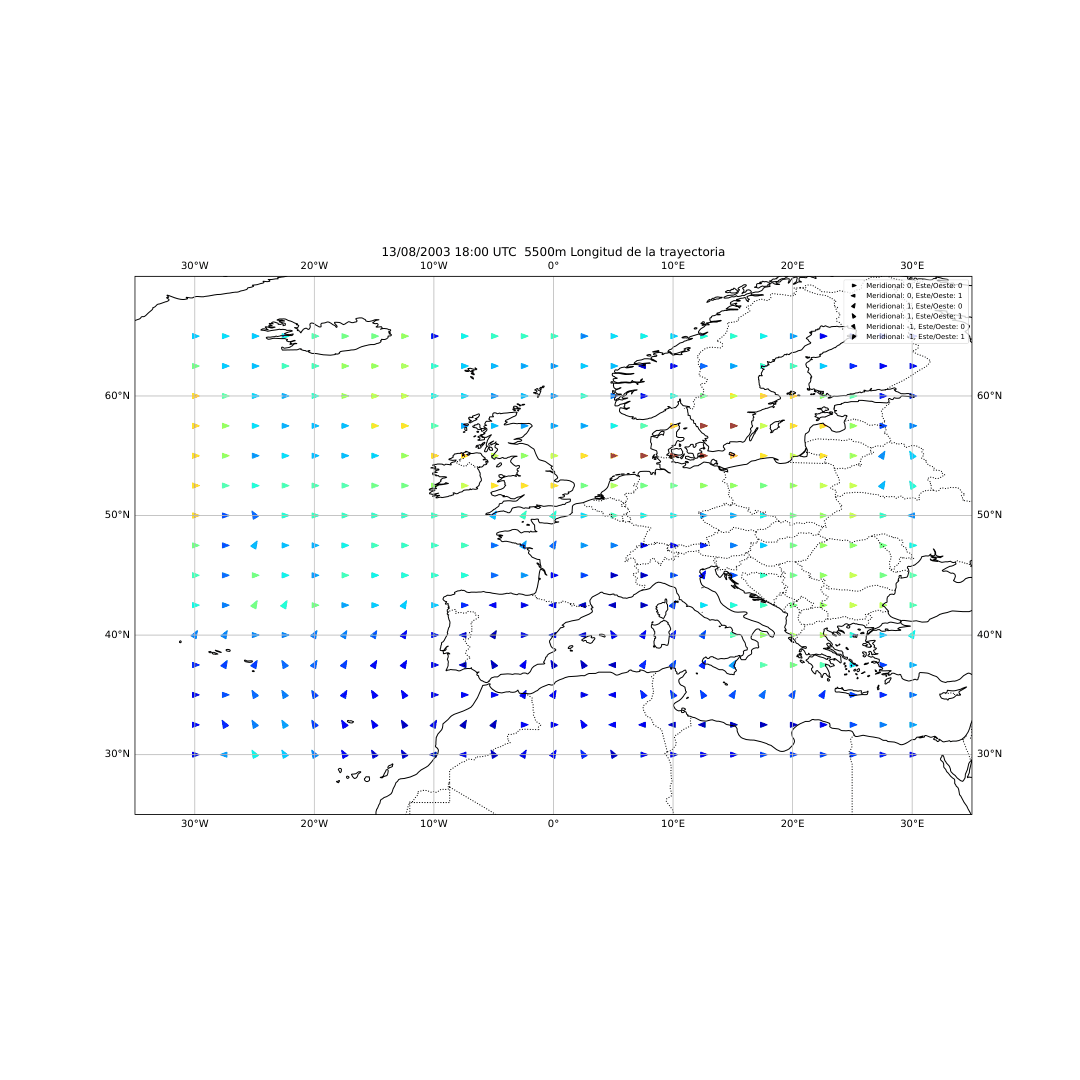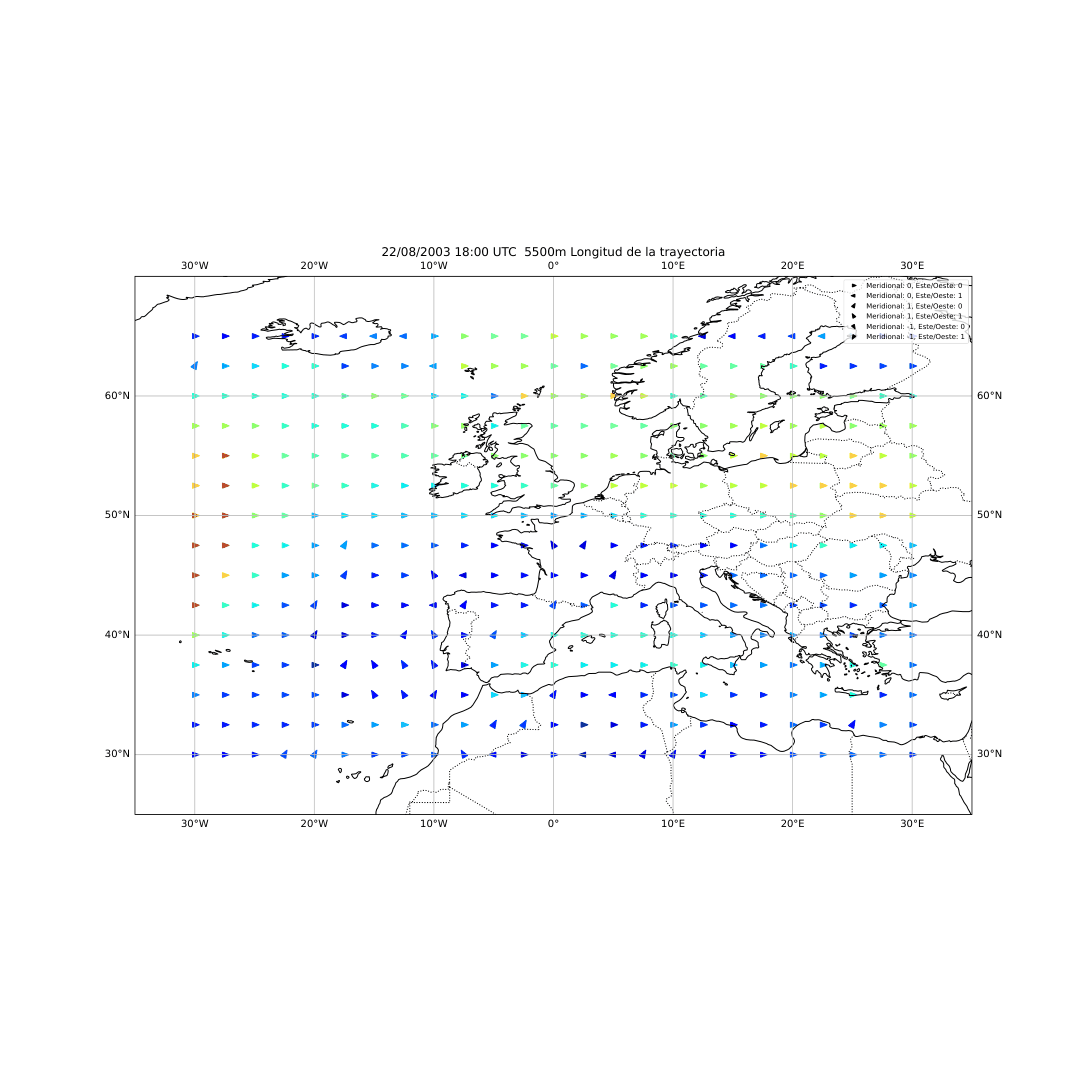
Figura 23
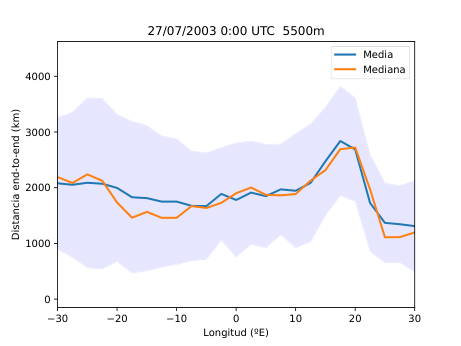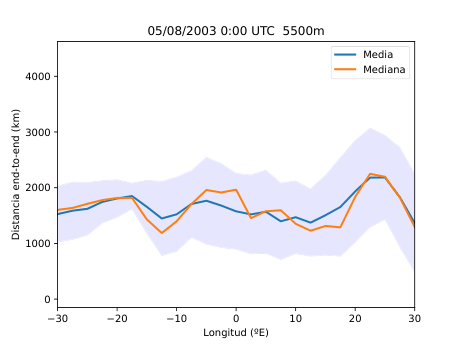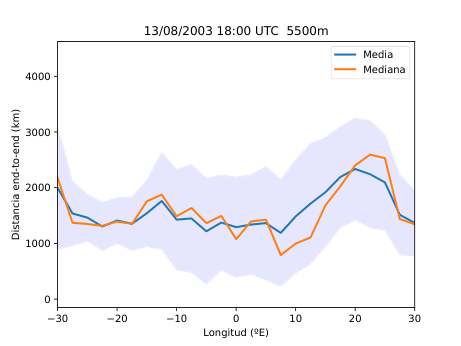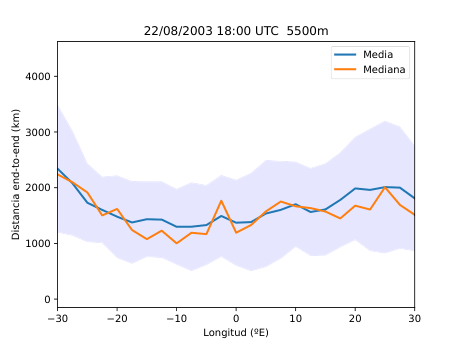
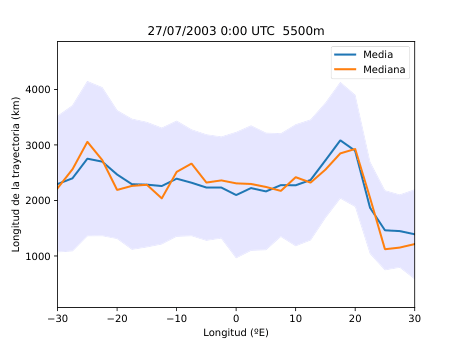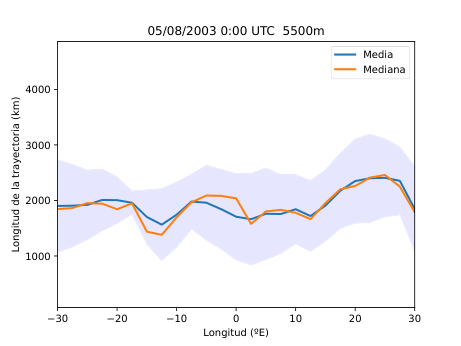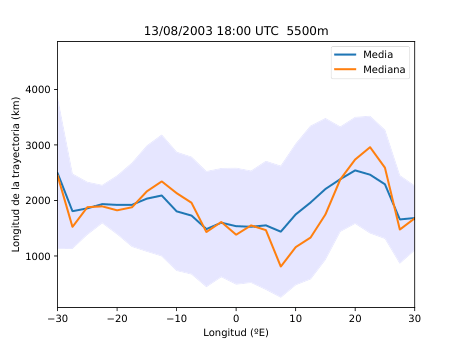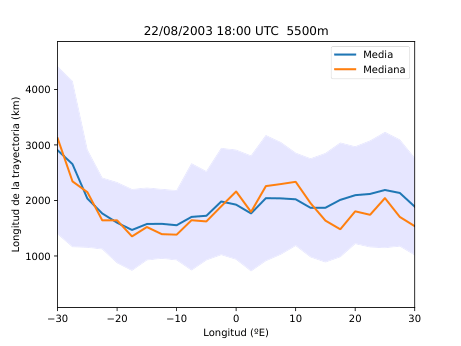
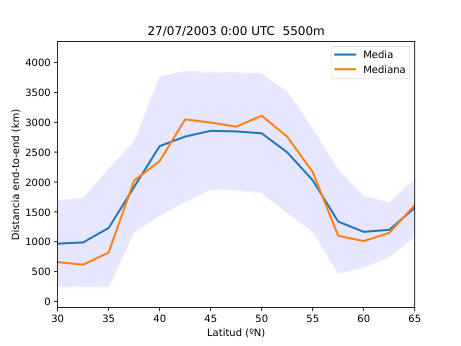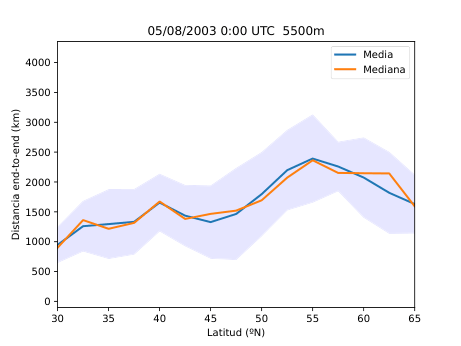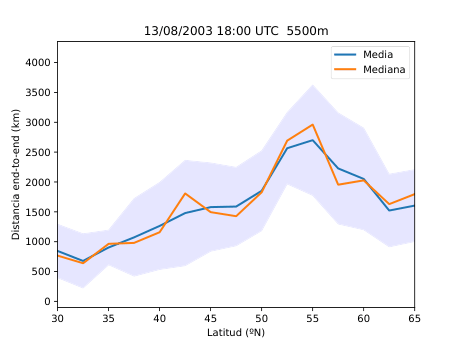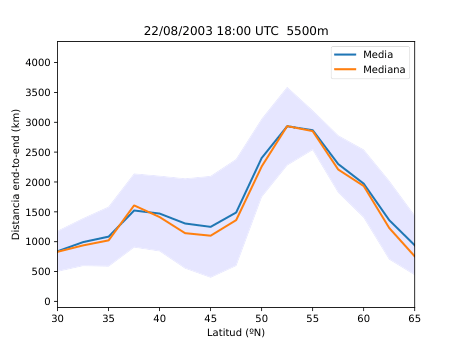
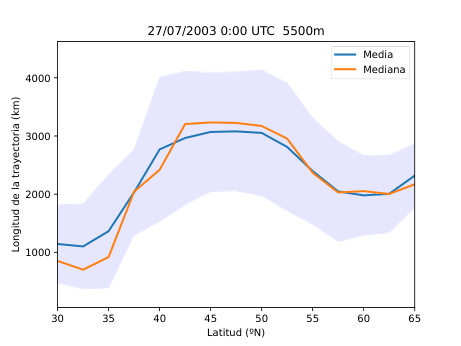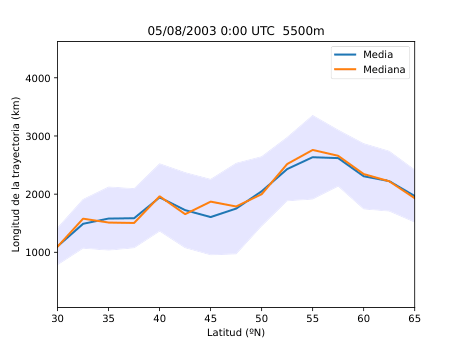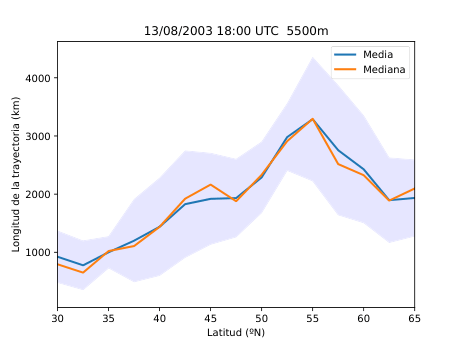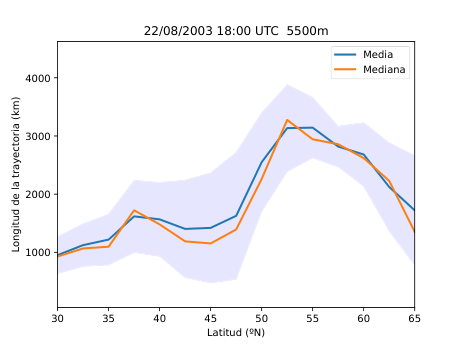
Figura 25

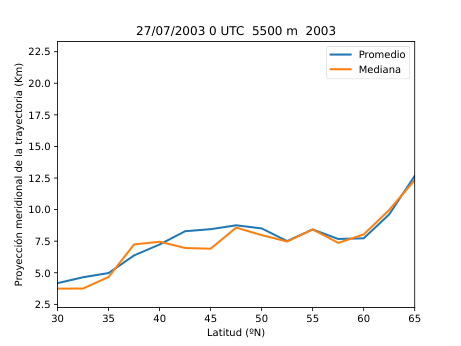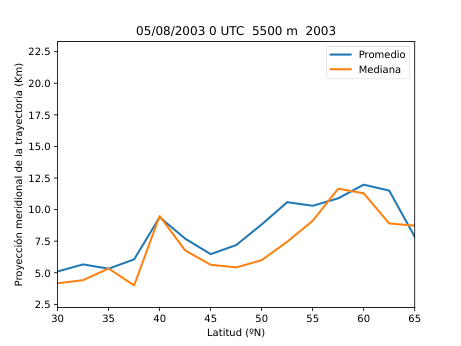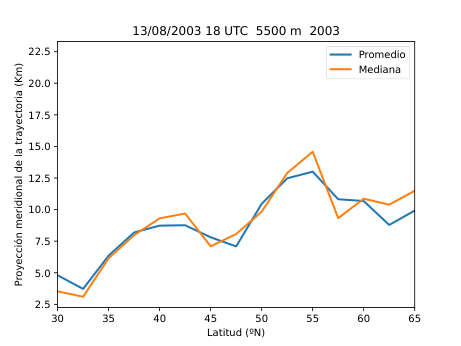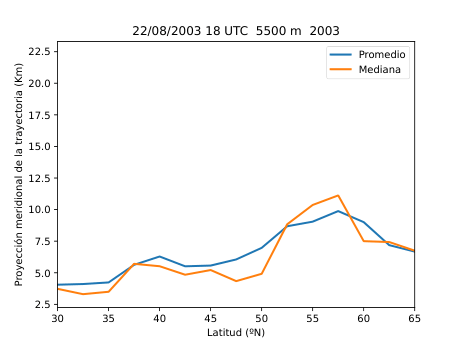
Figura 27